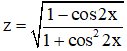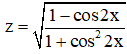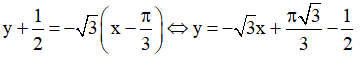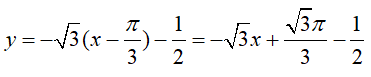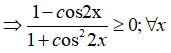Bài 1 (trang 178 SGK Đại số 11 Bài tập ): Cho hàm số y = cos2x.
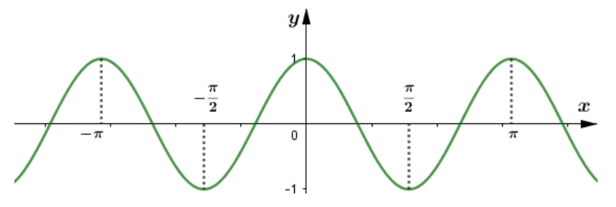
a) Chứng minh rằng cos 2(x + kπ) = cos 2x với mọi số nguyên k. Từ đó vẽ đồ thị (C) của hàm số y = cos 2x.
b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = π/3.
c) Tìm tập xác định của hàm số :
Bài giải:
a) + Hàm số y = cos x có chu kì 2π.
Do đó: cos 2.(x + kπ) = cos (2x + k2π) = cos 2x.
⇒ Hàm số y = cos 2x cũng tuần hoàn với chu kì π.
Từ đó suy ra
b. y = f(x) = cos 2x
⇒ y’ = f’(x) = (cos 2x)’ = -(2x)’.sin 2x = -2.sin 2x.
⇒ Phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = π/3 là:
c. Ta có: 1 – cos 2x = 2.sin2x ≥ 0.
Và 1 + cos22x > 0; ∀ x
⇒