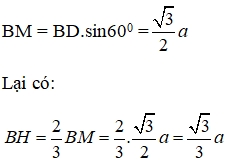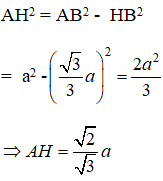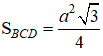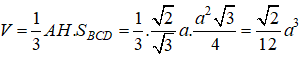Bài 1 (trang 25 SGK Hình học 12): Tính thể tích khối tứ diện đều cạnh a.
Bài giải:
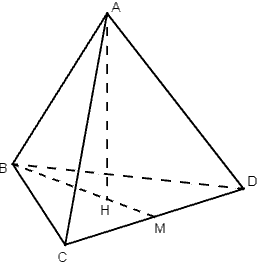
Gọi ABCD là tứ diện đều cạnh a.
Gọi H là tâm đường tròn ngoại tiếp tam giác BCD
⇒ HB = HC = HD nên H nằm trên trục đường tròn ngoại tiếp tam giác BCD. (1)
Lại có: AB = AC = AD vì ABCD là tứ diện đều
⇒ HA là trục đường tròn ngoại tiếp tam giác BCD
⇒ HA ⊥ (BCD)
Vì tam giác BCD là tam giác đều nên H đồng thời trọng tâm tam giác BCD. Gọi M là trung điểm của CD.
Xét tam giác BCD ta có:
Áp dụng định lí pytago vào tam giác vuông AHB ta được:
Diện tích tam giác đều BCD cạnh a là:
Do đó, thể tích khối tứ diện đều ABCD là: