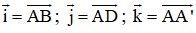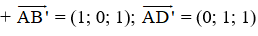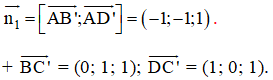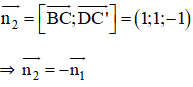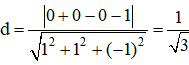Bài 10 (trang 81 SGK Hình học 12): giải bài toán sau đây bằng phương pháp tọa độ:

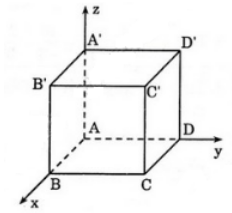
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1.

a) Chứng minh hai mặt phẳng (AB'D') và (BC'D) song song.

b)Tính khoảng cách giữa hai mặt phẳng nói trên.

Bài giải:

Chọn hệ trục tọa độ Oxyz có gốc O ≡ A; 

⇒ A(0; 0; 0) ; B(1; 0; 0); C(1; 1; 0); D(0; 1; 0).

A’(0; 0; 1); B’(1; 0; 1); C’(1; 1; 1); D’(0; 1; 1).

a)

⇒ Vectơ pháp tuyến của (AB’D’) là:

⇒ Vectơ pháp tuyến của (BC’D) là:

⇒ (AB’D’) // (BC’D).

b) Mặt phẳng (BC’D) có VTPT 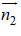 (1;1; -1) và qua B (1; 0;0) nên có phương trình:

1( x- 1) + 1( y – 0) - 1( z- 0)= 0 hay x + y - z - 1 = 0

Khoảng cách giữa hai mặt phẳng song song (AB’D’) và (BC’D) chính là khoảng cách từ A đến (BC’D) và bằng :