Bài 2 (trang 12 SGK Hình học 12): Chứng minh rằng một đa diện mà mỗi đỉnh của nó là đỉnh chung của một số lẻ mặt thì tổng số các đỉnh của nó phải là một số chẵn. Cho ví dụ.

Bài giải:

Cho khối đa diện G có các đỉnh là B₁, B₂,…, B_n và gọi M₁, M₂,…, M_n lần lượt là số các mặt của H nhận chúng làm đỉnh chung. Tổng số các cạnh của G là:

C = (M₁ + M₂ + … + M_n)/2

Vì C là số nguyên dương nên:

M₁ + M₂ + … + M_n là số chẵn.

Đồng thời M₁ ,M₂ , ..., M_n là n số tự nhiên lẻ nên tổng của chúng là số chẵn khi n chẵn.

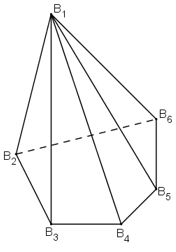
Ví dụ: Hình chóp ngũ giác B₁B₂B₃B₄B₅B₆ có: B₁ là đỉnh chung của 5 mặt bên. Mỗi đỉnh B₁, B₂, B₃, B₄, B₅, B₆ là đỉnh chung của ba mặt (hình trên).