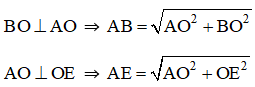Bài 4 (trang 18 SGK Hình học 12): Cho hình bát diện đều ABCDEF.
Chứng minh rằng:
a)Các đoạn thẳng AF, BD và CE đôi một vuông góc với nhau và cắt nhau tại trung điểm mỗi đường.
b)ABFD, AEFC và BCDE là những hình vuông.
Bài giải:
Giả sử bát diện đều ABCDEF có cạnh bằng a.
a) B, C, D, E cách đều A và F suy ra B, C, D, E cùng nằm trên mặt phẳng trung trực của đoạn thẳng AF
Trong mp (BCDE), ta có BC = CD = DE = EB (= a)
⇒ BCDE là hình thoi
⇒ BD ⊥ EC và BD, EC cắt nhau tại trung điểm mỗi đường.
Chứng minh tương tự ta suy ra AF và BD, AF và CE vuông góc nhau và cắt nhau tại trung điểm mỗi đường.
b) Gọi trung điểm BD, CE, AF là O.
Mà AB = AE (= a) ⇒ BO = OE ⇒ BD = EC
⇒ Hình thoi BCDE là hình vuông.
Chứng minh tương tự: ABFD, AEFC đều là hình vuông.
Chú ý : Hình thoi có hai đường chéo bằng nhau là hình vuông.