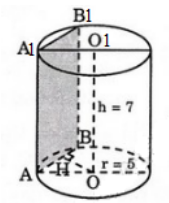
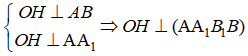Bài 5 (trang 39 SGK Hình học 12): Một hình trụ có bán kính đáy r = 5cm và có khoảng cách giữa hai đáy bằng 7cm.
a)Tính diện tích xung quanh của hình trụ và thể tích của khối trụ tạo nên.
b)Cắt khối trụ bởi một mặt phẳng song song với trục và cách trục 3cm. Hãy tính diện tích của thiết diện được tạo nên.
Bài giải:
a. Do khoảng cách hai đáy là nên chiều cao của hình trụ (đồng thời là độ dài đường sinh) là h = l = 7.
Diện tích xung quanh của hình trụ là:
Sxq = 2π.r.l = 2π.5.7 = 70π (cm2 ).
Thể tích của khối trụ được tạo nên là:
V = πr2.h = π.52.7 = 175π ( cm3 )
b. Mặt phẳng (P) song song với trục và cách trục 3cm, cắt hình trụ theo thiết diện là tứ giác AA1B1B.
Gọi H là trung điểm của AB.
Ta có
Suy ra: OH = d(O; (AA1B1B)), (1)
Lại có: OO1// mp (AA1B1B) , (2)
Từ (1) và (2) suy ra: OH = d(O; (AA1B1B)= d( OO1, (AA1B1B) ) = 3 cm
* Xét tam giác AOH vuông tại H ta có:
AH2 = AO2 - OH2 = 52 -32 = 16
⇒ AH = 4cm ⇒ AB = 2AH = 8cm
Diện tích của thiết diện cần tính là :
SAA1B1B = AB. AA1 = 8. 7 = 56 (cm2)