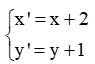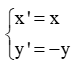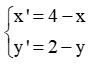Bài 1 (trang 125 SGK Hình học 11): Trong mặt phẳng tọa độ Oxy, cho các điểm A (1;1), B(0;3), C(2;4) .Xác định ảnh của tam giác ABC qua các phép biến hình sau.
(a)Phép tịnh tiến theo vector v = (2;1).
(b)Phép đối xứng qua trục Ox
(c)Phép đối xứng qua tâm I(2;1).
(d)Phép quay tâm O góc 90o.
(e)Phép đồng dạng có được bằng cách thực hiện liên tiếp phép đối xứng qua trụ Oy và phép vị tự tâm O tỉ số k = -2
Bài giải:
Gọi tam giác A'B'C' là ảnh của tam giác ABC qua phép biến hình trên.
(e)Phép đồng dạng có được bằng cách thực hiện liên tiếp phép đối xứng qua trục Oy và phép vị tự tâm O tỉ số k = -2
+) Qua phép đối xứng qua trục Oy biến tam giác ABC thành tam giác A1B1C1.
Do đó, tọa độ A1(-1; 1); B1(0; 3) và C1(-2; 4).
+) Qua phép vị tự tâm O tỉ số k = -2 biến tam giác A1B1C1 thành tam giác A2B2C2
Biểu thức tọa độ :
Tương tự; B2 (0; -6) và C2 (4; -8)
Vậy qua phép đối xứng trục Oy và phép vị tự tâm O tỉ số k = -2, biến các điểm A, B, C lần lượt thành
A2(2; -2); B2(0; -6) và C2 (4; -8).