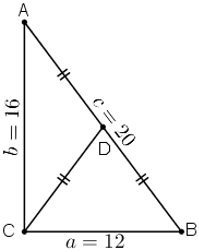
Bài 10 (trang 62 SGK Hình học 10): Cho tam giác ABC có a = 12, b = 16, c = 20. Tính diện tích S của tam giác, chiều cao h_a, bán kính R, r của các đường tròn ngoại tiếp, nội tiếp tam giác và đường trung tuyến m_a của tam giác

Bài giải:

Nhận xét: Tam giác ABC có a² + b² = c² nên vuông tại C.

+ Diện tích tam giác: S = 1/2.a.b = 1/2.12.16 = 96 (đvdt)

+ Chiều cao h_a: h_a = AC = b = 16.

+ Tâm đường tròn ngoại tiếp tam giác là trung điểm của AB.

Bán kính đường tròn ngoại tiếp R = AB /2 = c/2 = 10.

+ Bán kính đường tròn nội tiếp tam giác: S = p.r ⇒ r = S/p.

Mà S = 96, p = (a + b + c) / 2 = 24 ⇒ r = 4.

+ Đường trung tuyến m_a:

m_a² = (2.(b² + c²) – a²) / 4 = 292 ⇒ m_a = √292.