Bài 5 (trang 41 SGK Đại số 11): Giải các phương trình sau:
a. 2cos2x – 3cosx + 1 = 0
b. 25sin2x + 15sin2x + 9cos2x = 25
c. 2sinx + cosx = 1
d. sinx + 1,5cotx = 0
Bài giải:
a. 2cos2x – 3cosx + 1 = 0 (Phương trình bậc hai với ẩn cos x).
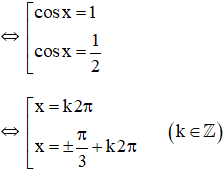
Vậy phương trình có tập nghiệm
b. 25sin2x + 15sin2x + 9cos2x = 25
⇔ 25sin2x + 15.2sinx.cosx + 9cos2x – 25 = 0
⇔ 25.(sin2x – 1) + 15.2.sinx.cosx + 9cos2x = 0
⇔ -25.cos2x + 30sinx.cosx + 9cos2x = 0
⇔ 16.cos2x – 30.sinx.cosx = 0
⇔ 2.cosx.(8cosx – 15sinx) = 0
+ Giải (1): 2.cos x = 0 ⇔ cos x = 0
+ Giải (2): 8.cos x – 15.sin x = 0
⇔ 8.cos x = 15.sin x.
Vậy phương trình có tập nghiệm
c. 2.sin x + cos x = 1
Vì nên tồn tại α thỏa mãn
(1) trở thành:
Vậy phương trình có nghiệm {k2π; 2α+k2π/k ∈ Z }
với α thỏa mãn
Phương trình trên là phương trình bậc nhất đối với sin và cos.
Phương pháp giải: Xem lại kiến thức áp dụng bài 5 trang 37.
d. Điều kiện x ≠ kπ ∀ k ∈ Z
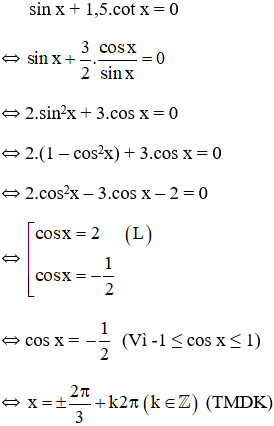
Vậy phương trình có tập nghiệm


