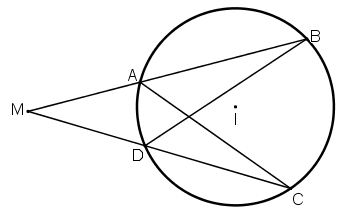
Bài 5 (trang 49 SGK Hình học 12): Từ một điểm M nằm ngoài mặt cầu (O; R), vẽ hai đường thẳng cắt mặt cầu lần lượt tại A, B và C, D.
a) Chứng minh rằng MA.MB = MC.MD
b) Gọi MO = d. Tính MA.MB theo R và d.
Bài giải:
a) Hai đường thẳng MAB và MCD giao nhau xác định một mặt phẳng (P). Mặt phẳng (P) cắt mặt cầu theo giao tuyến là đường tròn (C), ngoại tiếp tứ giác phẳng ABCD.
Xét ΔMAC và ΔMDB có:
⇒ MA.MB = MC.MD (đpcm).
b) Giả sử đường thẳng MO cắt mặt cầu tại P và Q.
Theo kết quả phần a) ta cùng có:
MA.MB = MP.MQ
Mà MP.MQ = (MO – OP)(MO + OQ) = (d – r)(d + r) = d2 – r2.
Vậy MA.MB = d2 – r2.