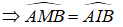Bài 6 (trang 49 SGK Hình học 12): Cho mặt cầu (O; R) tiếp xúc với mặt phẳng (P) tại I. Gọi M là một điểm nằm trên mặt cầu nhưng không phải là điểm đối xứng với I qua tâm O. Từ M ta kẻ hai tiếp tuyến của mặt cầu cắt (P) tại A và B. Chứng minh rằng góc (AMB)= góc (AIB)
Bài giải:
* Do mặt cầu S(O; r) tiếp xúc với mp (P) tại I nên: OI ⊥ (P) ⇒ OI ⊥ IA
Suy ra, AI là tiếp tuyến của mặt cầu đã cho tại điểm I.
Ta có AM và AI là hai tiếp tuyến cắt nhau tại A của mặt cầu nên:
AM = AI ( tính chất hai tiếp tuyến cắt nhau)
* Tương tự có BM = BI.
* Xét hai tam giác AMB và tam giác AIB có:
AM = AI
BM = BI
AB chung
Suy ra: ∆ AMB = ∆ AIB ( c.c.c)