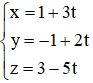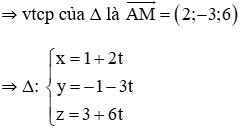Bài 7 (trang 92 SGK Hình học 12): Cho điểm A(-1; 2; -3), vectơ a→ = (6; -2; -3) và đường thẳng d có phương trình: 

a) Viết phương trình mặt phẳng (α) chứa điểm A và vuông góc với giá của a→.

b) Tìm giao điểm của d và (α).

c) Viết phương trình đường thẳng Δ đi qua điểm A, vuông góc với a→ và cắt đường thẳng d.

Bài giải:

a) (α) vuông góc với giá của a→

⇒ (α) nhận a→ là 1 vtpt.

(α) đi qua A(-1; 2; -3)

⇒ (α): 6x – 2y – 3z + 1 = 0.

b) Gọi giao điểm của d và (α) là M.

M ∈ d ⇒ M(1 + 3t; -1 + 2t; 3 – 5t).

M ∈ (α) ⇒ 6(1 + 3t) – 2(-1 + 2t) – 3(3 – 5t) + 1 = 0

⇔ 29t = 0

⇔ t = 0

⇒ M(1; -1; 3).

c) (α) ⊥ a→

Δ ⊥ a→

⇒ Δ song song hoặc nằm trong (α).

Mà Δ và (α) cùng đi qua A

⇒ Δ ⊂ (α)

Δ cắt d ⇒ Δ cắt d tại M

⇒ Δ chính là đường thẳng AM.