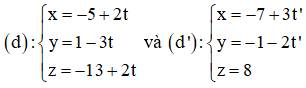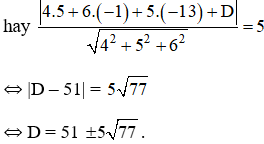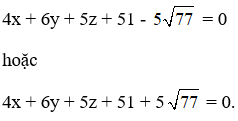Bài 8 (trang 93 SGK Hình học 12): Viết phương trình mặt phẳng (α) tiếp xúc với mặt cầu (S):

(S): x² + y² + z² – 10x + 2y +26z + 170 = 0

và song song với hai đường thẳng:

Bài giải:

+ Mặt cầu (S): x² + y² + z² – 10x + 2y +26z + 170 = 0

⇔ (x – 5)² + (y + 1)² + (z + 13)² = 25

Vậy (S) có tâm I(5; -1; -13), bán kính R = 5.

+ (α) song song với d và d’

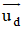
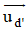
⇒ (α) nhận vtcp của d và d’ là  = (2; -3; 2) và  = (3 ; -2 ; 0) là các vtcp

⇒ (α) nhận 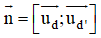 = (4; 6; 5) là vtpt

⇒ (α): 4x + 6y + 5z + D = 0.

(α) tiếp xúc với (S)

⇒ d(I; α) = R

Vậy có hai mặt phẳng thỏa mãn là: