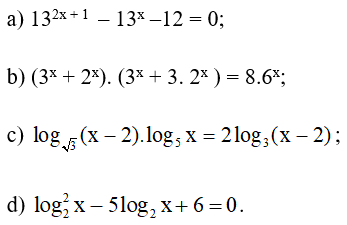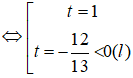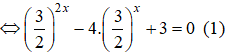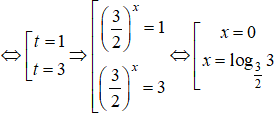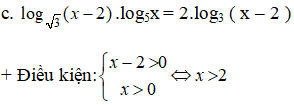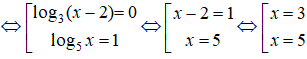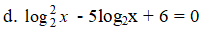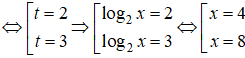Bài 9 (trang 147 SGK Giải tích 12): Giải các phương trình sau:
Bài giải:
a. 132x+1 – 13x - 12 = 0
⇔ 13. 132x – 13x – 12 = 0 (1)
Đặt t = 13x (t > 0), khi đó (1) trở thành:
13t2 - t - 12 = 0
Với t = 1 thì 13x = 1 ⇔ x = 0
Vậy nghiệm của phương trình đã cho là x = 0
b. (3x + 2x ). (3x +3. 2x ) = 8. 6x
⇔ 32x + 3. 3x. 2x + 2x. 3x + 3. 22x – 8.6x = 0
⇔ 32x +4. 3x. 2x - 8.2x. 3x + 3. 22x = 0
⇔ 32x – 4. 3x.2x + 3.22x = 0 (*)
Chia cả hai vế của phương trình trên cho 22x ta được:
Đặt 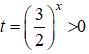
t2 - 4t+ 3 = 0
+ Ta có: 2log3 (x - 2). log5x - 2.log3 ( x - 2) = 0
⇔ 2. log3 (x - 2) ( log5 x - 1) = 0
Kết hợp điều kiện , vậy nghiệm phương trình đã cho là x = 3; x = 5.
+ Điều kiện: x > 0
Đặt t = log2x, khi đó phương trình đã cho trở thành:
t2 – 5t + 6 = 0
Kết hợp với điều kiện, nghiệm phương trình đã cho là x = 4; x = 8.