Bài 1 (trang 18 SGK Giải tích 12): Áp dụng Quy tắc 1, hãy tìm các điểm cực trị của các hàm số sau:
a) y = 2x3 + 3x2 - 36x - 10
Bài giải:
a) TXĐ: D = R
y' = 6x2 + 6x - 36
y' = 0 ⇔ x = -3 hoặc x = 2
Bảng biến thiên:
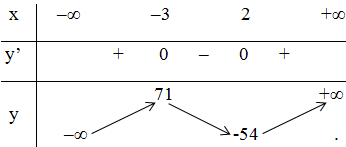
Kết luận :
Hàm số đạt cực đại tại x = -3 ; yCĐ = 71
Hàm số đạt cực tiểu tại x = 2; yCT = -54.
b) TXĐ: D = R
y'= 4x3 + 4x = 4x(x2 + 1) = 0;
y' = 0 ⇔ x = 0
Bảng biến thiên:
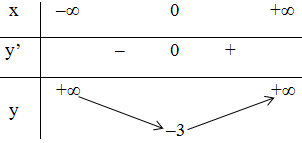
Vậy hàm số đạt cực tiểu tại x = 0; yCT = -3
hàm số không có điểm cực đại.
c) TXĐ: D = R \ {0}
y' = 0 ⇔ x = ±1
Bảng biến thiên:
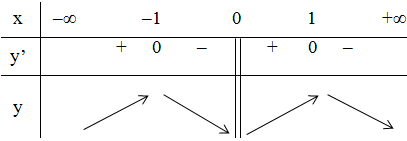
Vậy hàm số đạt cực đại tại x = -1; yCĐ = -2;
hàm số đạt cực tiểu tại x = 1; yCT = 2.
d) TXĐ: D = R
y'= (x3)’.(1 – x)2 + x3.[(1 – x)2]’
= 3x2.(1 – x)2 + x3.2(1 – x).(1 – x)’
= 3x2(1 – x)2 - 2x3(1 – x)
= x2.(1 – x)(3 – 5x)
y' = 0 ⇔ x = 0; x = 1 hoặc x = 3/5
Bảng biến thiên:
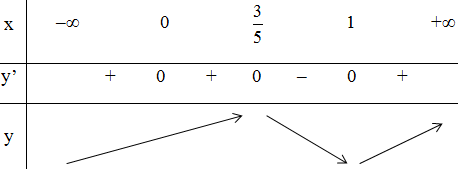
Vậy hàm số đạt cực đại tại x =
hàm số đạt cực tiểu tại xCT = 1.
(Lưu ý: x = 0 không phải là cực trị vì tại điểm đó đạo hàm bằng 0 nhưng đạo hàm không đổi dấu khi đi qua x = 0.)
e) Tập xác định: D = R.
Bảng biến thiên:
Vậy hàm số đạt cực tiểu tại x = 1/2.


